2023. 2. 19

© WONKOOK LEE

행렬의 개념과 연산 및 코딩테스트

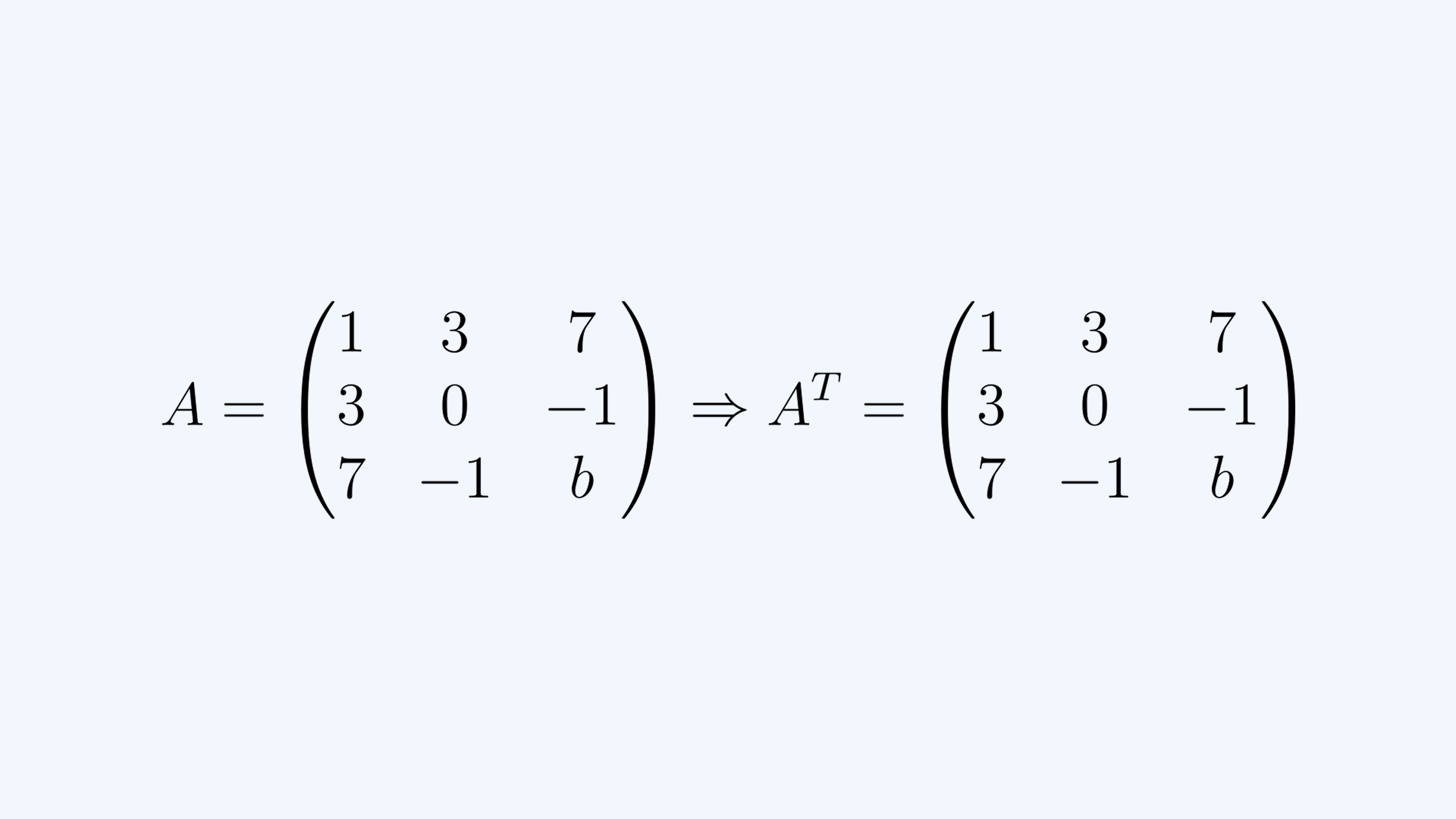
들어가며

행렬(Matrix)은 컴퓨터 공학과 프로그래밍에서 중요한 개념 중 하나입니다. 특히, 그래픽 처리, 데이터 분석, 머신러닝, 게임 개발 등 다양한 분야에서 사용되며, 코딩 테스트에서도 종종 출제됩니다. 또한, 선형대수학에서 중요한 개념이므로, 이를 잘 이해하면 문제 해결 능력을 크게 향상시킬 수 있습니다.

이 문서는 행렬의 기본 개념과 주요 연산에 대해 설명합니다. 처음 접하는 분들도 쉽게 이해할 수 있도록 최대한 직관적으로 설명하겠습니다.

---

기본 용어

행렬(matrix)은 숫자 또는 문자를 직사각형 형태로 배열한 것입니다. 가로줄을 행(row), 세로줄을 열(column) 이라고 합니다.

예시:

$\begin{bmatrix} 1 & 3 & 2 \\ 5 & 1 & 7 \end{bmatrix}$

위 행렬은 $2 \times 3$ 행렬이라고 하며, $7$은 $(2,3)$ 성분입니다.

행렬 표기

행렬은 일반적으로 다음과 같이 나타냅니다.

$A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{bmatrix}$

각 성분은 $a_{ij}$ 형태로 표기합니다.

$\begin{bmatrix} 3 & 5 \\ -1 & 7 \end{bmatrix}$

위 행렬은 $2 \times 2$ 행렬 또는 2차 정사각 행렬(square matrix) 입니다.

---

행렬의 종류

전치 행렬 (Transpose Matrix)

전치 행렬(transpose matrix)은 원래 행렬의 행과 열을 바꾼 행렬입니다. 보통 $A^{\top}$ 또는 $A^T$로 표기합니다.

예시:

$A = \begin{bmatrix} 1 & 2 & 4 \\ 5 & 3 & 7 \end{bmatrix} \Rightarrow A^T = \begin{bmatrix} 1 & 5 \\ 2 & 3 \\ 4 & 7 \end{bmatrix}$

전치 행렬은 데이터 변환 및 머신러닝에서 중요한 역할을 합니다. 예를 들어, 벡터의 방향을 변환하거나 행렬 연산을 최적화하는 데 사용됩니다.

대칭 행렬 (Symmetric Matrix)

대칭 행렬은 전치 행렬과 자기 자신이 같을 때 성립합니다: $A = A^{\top}$

$A = \begin{bmatrix} 1 & 3 \\ 3 & a \end{bmatrix} \Rightarrow A^T = \begin{bmatrix} 1 & 3 \\ 3 & a \end{bmatrix}$

대칭 행렬은 그래프 이론이나 공학에서 자주 사용되며, 물리학에서도 응력(stress)과 관련된 행렬로 활용됩니다.

대각 행렬 (Diagonal Matrix)

대각 성분이 아닌 모든 성분이 $0$인 행렬을 대각 행렬(diagonal matrix) 이라고 합니다.

$\begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 3 \end{bmatrix}$

• 대각 성분은 $0$이어도 상관없습니다.
• 대각 행렬은 항상 대칭 행렬입니다.
• 연산이 단순하여 컴퓨터 연산 속도를 빠르게 하기 위한 최적화된 구조로 사용됩니다.

단위 행렬 (Identity Matrix)

대각 성분만 $1$이고 나머지는 $0$인 행렬을 단위 행렬(identity matrix) 이라고 합니다. 단위 행렬 $I$는 행렬 곱셈에서 곱셈 항등원의 역할을 합니다.

$I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, \quad I = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$

단위 행렬은 행렬 곱셈에서 다음과 같은 항등원 역할을 합니다.

$A \cdot I = I \cdot A = A$

이는 일반적인 수에서 $1$이 곱셈의 항등원 역할을 하는 것과 같은 개념입니다.

영행렬 (Zero Matrix)

모든 성분이 $0$인 행렬을 영행렬(zero matrix) 이라고 합니다.

$\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}, \quad \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}$

영행렬은 덧셈에서 항등원의 역할을 하며, 신호 처리나 선형 시스템에서 중요한 역할을 합니다.

---

행렬의 연산

행렬의 비교: $A = B$

두 행렬의 같은 위치의 성분이 모두 같을 때 $A = B$ 입니다.

$\begin{bmatrix} 1 & x \\ 2 & 3 \end{bmatrix} = \begin{bmatrix} 1 & 2 \\ 2 & y \end{bmatrix}$

이때, $x = 2, y = 3$ 입니다.

행렬의 실수배 (Scalar Multiplication)

행렬의 모든 성분에 특정한 숫자(스칼라)를 곱하는 연산입니다.

$3A = \begin{bmatrix} 6 & 3 \\ 15 & 9 \end{bmatrix}$

행렬의 덧셈 (Addition)과 뺄셈 (Subtraction)

같은 크기의 행렬끼리만 가능합니다.

$A + B = \begin{bmatrix} 1 & 5 \\ 6 & 5 \end{bmatrix}$

$A - B = \begin{bmatrix} 3 & -3 \\ 4 & 1 \end{bmatrix}$

행렬의 곱셈 (Matrix Multiplication)

행렬 곱셈은 일반적인 덧셈이나 뺄셈과 다릅니다. 같은 위치에 있는 성분끼리 연산하는 것이 아니라, 왼쪽 행렬의 행과 오른쪽 행렬의 열을 대응시켜 계산합니다.

예제 1: $2 \times 2$ 행렬 곱셈

$\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \times \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix}$

각 행과 열의 성분을 곱하고 합하여 새로운 행렬을 만듭니다.

$= \begin{bmatrix} (1 \cdot 5 + 2 \cdot 7) & (1 \cdot 6 + 2 \cdot 8) \\ (3 \cdot 5 + 4 \cdot 7) & (3 \cdot 6 + 4 \cdot 8) \end{bmatrix}$

$= \begin{bmatrix} 19 & 22 \\ 43 & 50 \end{bmatrix}$

위 연산에서 결과 행렬의 각 성분은 왼쪽 행렬의 행과 오른쪽 행렬의 열을 곱한 값들의 합입니다.

예제 2: $2 \times 2$ 행렬과 $2 \times 1$ 행렬의 곱셈

$\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \times \begin{bmatrix} 5 \\ 6 \end{bmatrix}$

이 경우, 결과 행렬의 크기는 $(2 \times 1)$이 됩니다.

$= \begin{bmatrix} (1 \cdot 5 + 2 \cdot 6) \\ (3 \cdot 5 + 4 \cdot 6) \end{bmatrix}$

$= \begin{bmatrix} 17 \\ 39 \end{bmatrix}$

예제 3: $2 \times 3$ 행렬과 $3 \times 2$ 행렬의 곱셈

$\begin{bmatrix} 4&-2&1\\ 0&2&3\\ \end{bmatrix} \times \begin{bmatrix} 0&-3\\ -2&1\\ 1&4\\ \end{bmatrix}$

$= \begin{bmatrix} (4 \cdot 0+(-2) \cdot (-2)+1 \cdot 1) & (4 \cdot (-3)+(-2) \cdot 1+1 \cdot 4) \\ (0 \cdot 0+2 \cdot (-2)+3 \cdot 1) & (0 \cdot (-3)+2 \cdot 1+3 \cdot 4) \\ \end{bmatrix}$

$= \begin{bmatrix} 5&-10\\ -1&14\\ \end{bmatrix}$

설명:

• 첫 번째 행과 첫 번째 열을 곱한 값이 첫 번째 행, 첫 번째 열의 성분이 됩니다.
  $C_{11} = A_{11} \cdot B_{11} + A_{12} \cdot B_{21} + A_{13} \cdot B_{31}$

• 첫 번째 행과 두 번째 열을 곱한 값이 첫 번째 행, 두 번째 열의 성분이 됩니다.
  $C_{12} = A_{11} \cdot B_{12} + A_{12} \cdot B_{22} + A_{13} \cdot B_{32}$

• 두 번째 행과 첫 번째 열을 곱한 값이 두 번째 행, 첫 번째 열의 성분이 됩니다.
  $C_{21} = A_{21} \cdot B_{11} + A_{22} \cdot B_{21} + A_{23} \cdot B_{31}$

• 두 번째 행과 두 번째 열을 곱한 값이 두 번째 행, 두 번째 열의 성분이 됩니다.
  $C_{22} = A_{21} \cdot B_{12} + A_{22} \cdot B_{22} + A_{23} \cdot B_{32}$

이처럼 각 행과 열을 대응하여 곱하고 더하는 방식으로 행렬의 곱셈을 수행합니다.

행렬 곱셈의 일반적인 규칙

• 행렬 곱셈이 성립하려면 왼쪽 행렬의 열 개수와 오른쪽 행렬의 행 개수가 같아야 합니다.
• 결과 행렬의 크기는 왼쪽 행렬의 행 개수 × 오른쪽 행렬의 열 개수가 됩니다.

즉, 다음과 같은 수식을 만족해야 합니다.

 

$A (m \times n) \times B (n \times r) = C (m \times r)$

위 개념을 잘 이해하면, 프로그래밍에서 행렬 연산을 다룰 때 매우 유용하게 활용할 수 있습니다.

---

코딩테스트: 행렬의 곱셈

 

행렬의 곱셈은 코딩 테스트에서 자주 출제되는 문제 유형 중 하나입니다. 특히 2차원 배열을 다루는 능력, 중첩 반복문을 활용한 연산 최적화, 그리고 행렬 곱셈의 기본 개념을 평가하는 데 사용됩니다.

문제

2차원 행렬 $A$와 $B$를 입력받아 행렬 $A$에 행렬 $B$를 곱한 결과를 반환하는 solution() 함수를 완성하세요.

제약조건

• 행렬 $A$, $B$의 행과 열의 길이는 2 이상 100 이하입니다.
• 행렬 $A$, $B$의 데이터는 -10 이상 20 이하인 자연수입니다.

문제 풀이 (JavaScript)

function solution(A, B) {
  // A의 행(row) 개수
  const m = A.length;
  // A의 열(column) 개수 (B의 행 개수와 같아야 함)
  const n = A[0].length;
  // B의 열(column) 개수 (결과 행렬의 열 개수)
  const p = B[0].length;

  // 행렬 곱셈이 가능한지 확인 (A의 열 개수와 B의 행 개수가 일치해야 함)
  if (n !== B.length) throw new Error("행렬의 곱이 성립되지 않음");

  // 결과 행렬 C 초기화 (m x p 크기의 2차원 배열, 0으로 채워진 상태)
  const C = Array.from({ length: m }, () => new Array(p).fill(0));

  // 행렬 곱셈 수행
  for (let i = 0; i < m; i++) {
    // A의 행을 반복
    for (let j = 0; j < p; j++) {
      // B의 열을 반복
      for (let k = 0; k < n; k++) {
        // A의 열과 B의 행을 반복 (곱셈 연산)
        C[i][j] += A[i][k] * B[k][j]; // A의 i행 k열 원소와 B의 k행 j열 원소를 곱한 값을 더함
      }
    }
  }

  // 결과 행렬 반환
  return C;
}

코드 설명

1. $m, n, p$는 각각 $A$의 행 개수, $A$의 열 개수 ($B$의 행 개수), $B$의 열 개수를 나타냄.

2. n !== B.length 조건을 검사하여 행렬 곱셈이 가능한지 확인.

3. $C$는 결과 행렬이며, $m \times p$ 크기의 배열을 $0$으로 초기화.

4. 3중 for문을 이용하여 행렬 곱셈 수행:

   • i는 $A$의 행 인덱스.
   • j는 $B$의 열 인덱스.
   • k는 $A$의 열과 $B$의 행을 연결하는 인덱스.
   • C[i][j] += A[i][k] * B[k][j]를 통해 행렬 원소를 누적하여 계산.

5. 최종적으로 $C$를 반환.